[最も好ましい] 円錐 高さ 公式 129874-円錐 表面積 公式 高さ
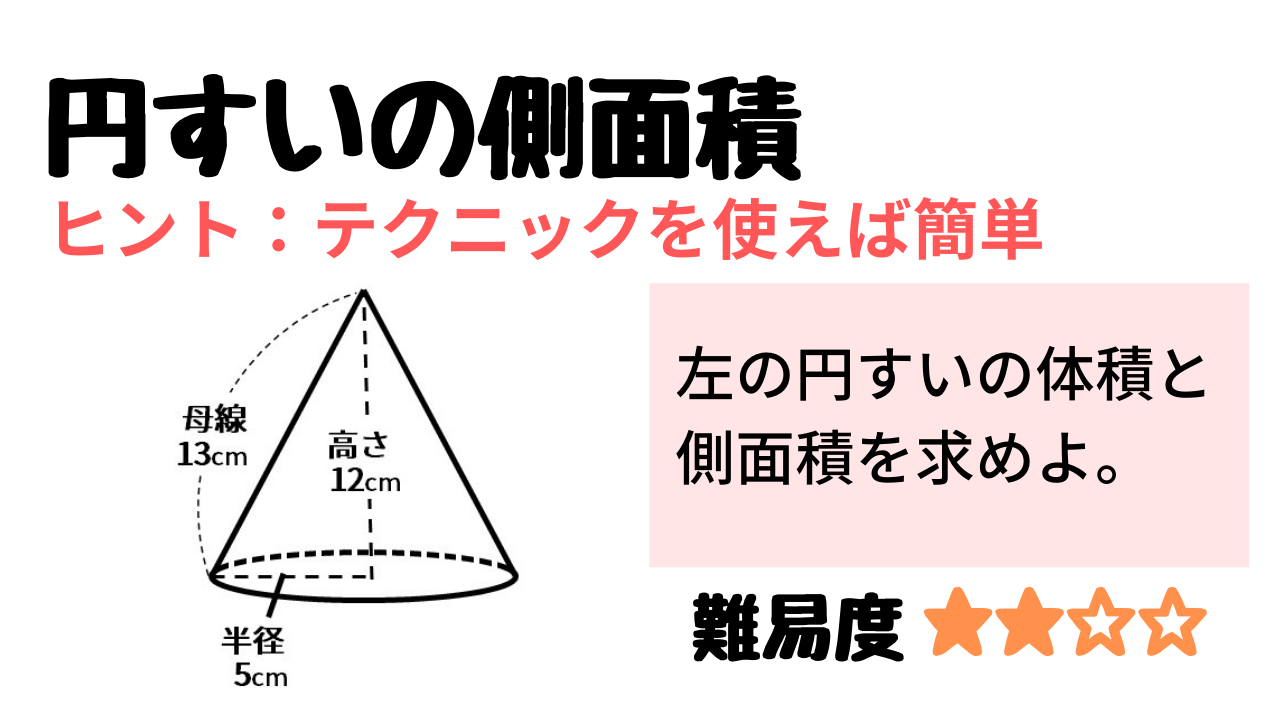
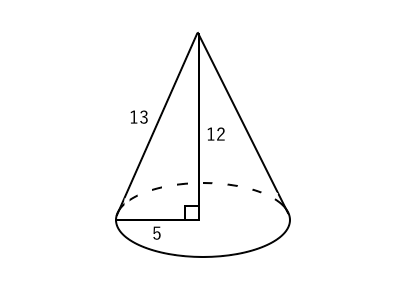
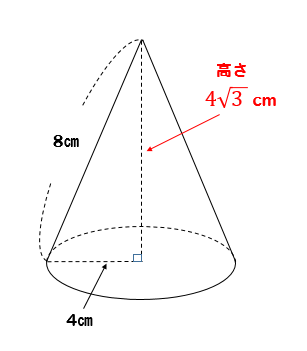
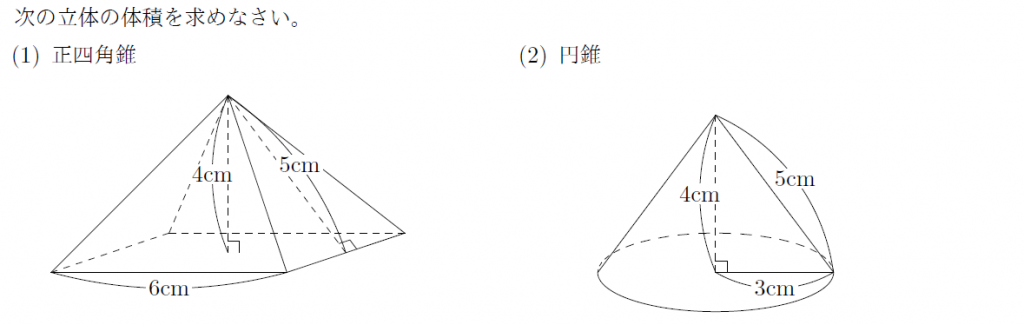
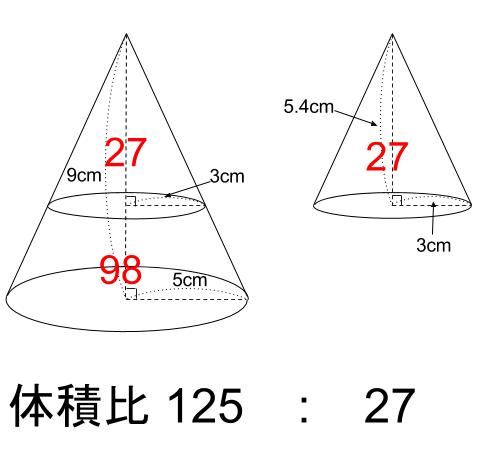
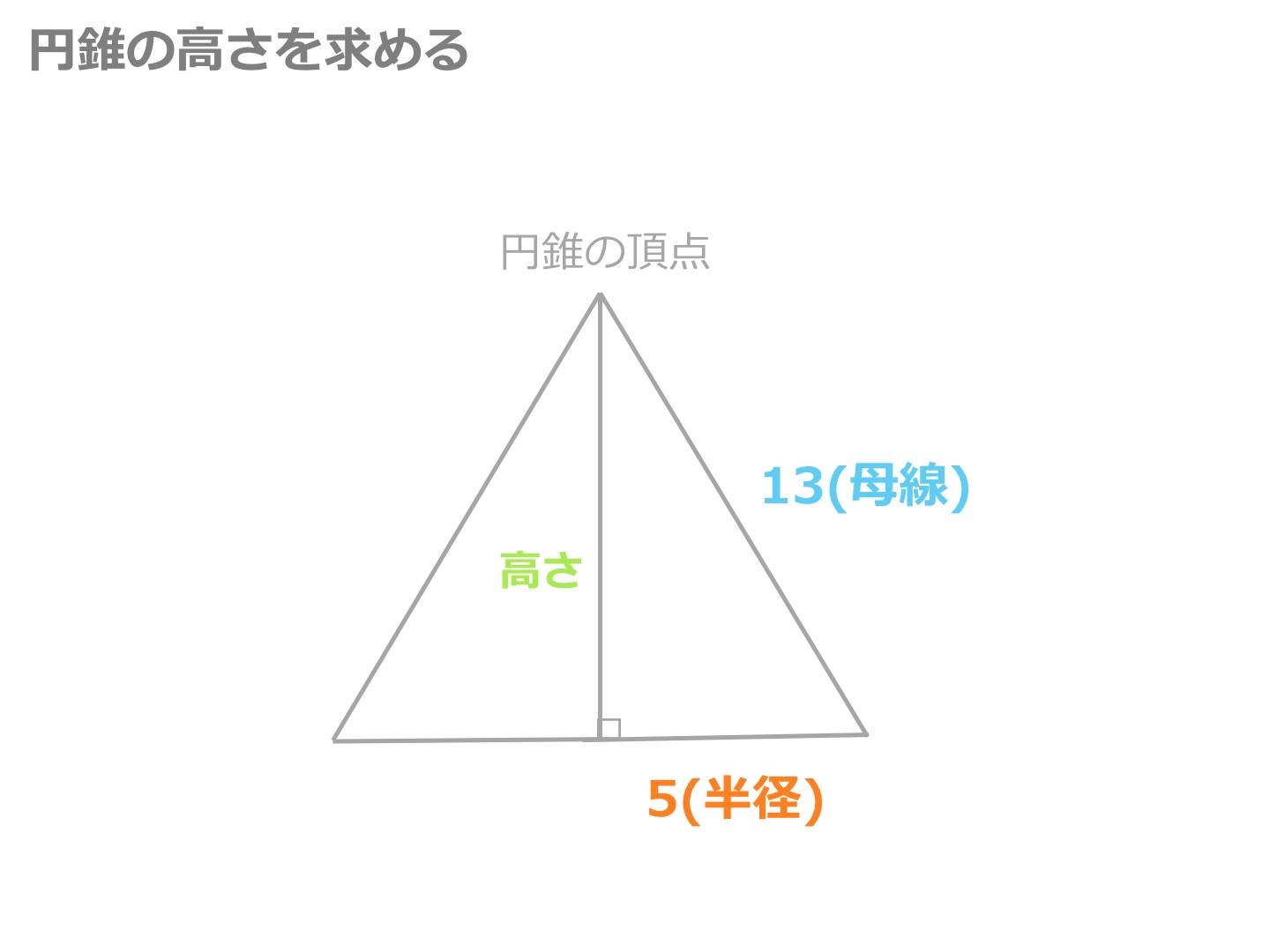
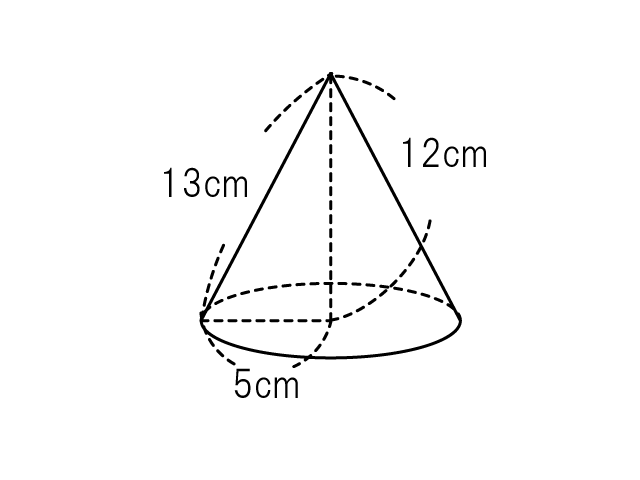
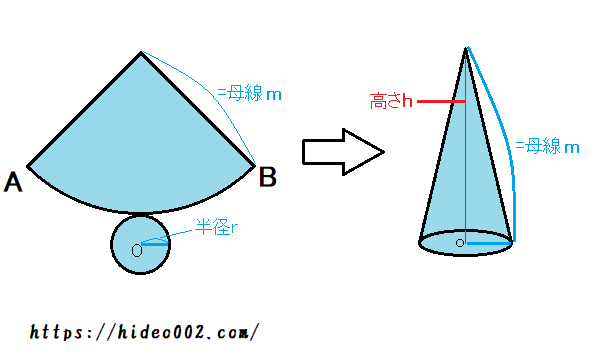
円すいの体積の公式 底円の半径を r 、高さを h とすると 上図の円錐の体積は 体 積 底 面 積 高 さ 体積 V = 底面積 × 高さ × 1 3 = r × r × 314 × h × 1 3 公式を利用した解答 展開図から、円すいを作る 展開図を組み立てて、できる 円すい は このままでは、 高さが無い ので、円すいの体積を求めることが出来ません 高さは、赤い直角三角形に注目する この円すいの赤い部分に注目します。
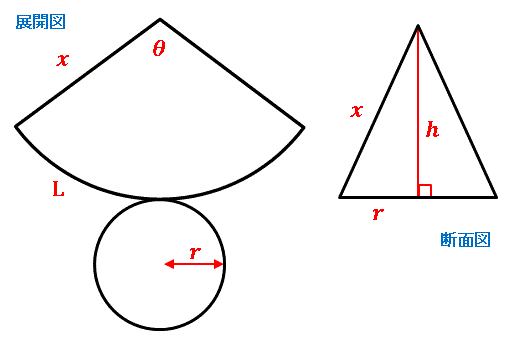
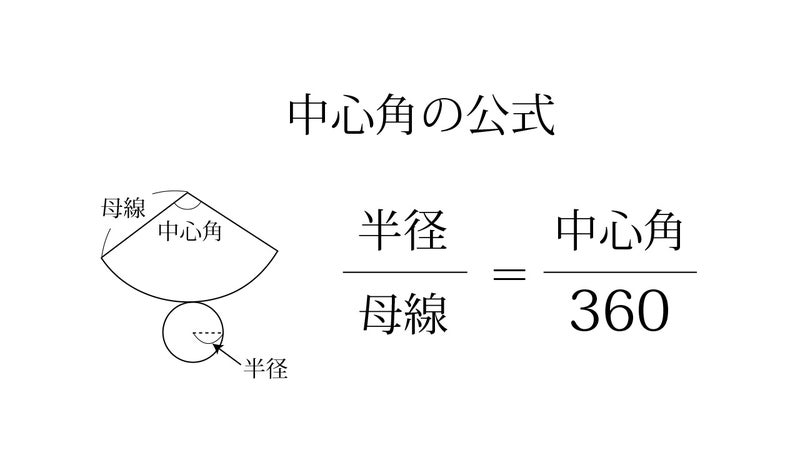
円錐 表面積 公式 高さ-(底面の半径が 3 c m 、母線の長さが 8 c m ) r = l × x 360 という公式で、 r = 3 、 l = 8 とすると、 3 = 8 × x 360 となります。 よって、中心角は、 x = 360 × 3 8 = 135 ∘ となります。 まとめ r = l × x 360 という公式さえ覚えておけば、上記のような3つのタイプの問題は全て解くことができます。 次回は 半球の体積と表面積を計算する を解説します。A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周 (近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐
円錐 表面積 公式 高さのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  |  |
「円錐 表面積 公式 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「円錐 表面積 公式 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「円錐 表面積 公式 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  | |
「円錐 表面積 公式 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「円錐 表面積 公式 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「円錐 表面積 公式 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「円錐 表面積 公式 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「円錐 表面積 公式 高さ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
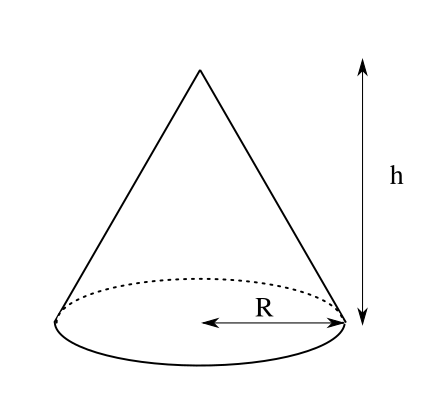
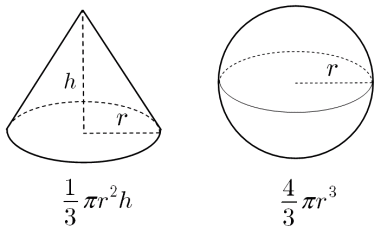
円錐の高さを求める公式はありますか? 円錐の体積の公式を変形!!V=SXh÷3よりh=3V÷SV:体積h:高さS:底面積 円錐の高さを求める公式はありますか? 円錐の体積の公式を変形!円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径です。 円錐の体積を求めるには、この公式に底面の半径 r と高さ h を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています。 もくじ 円錐の体積
Incoming Term: 円錐 高さ 公式, 円錐 表面積 公式 高さ,
コメント
コメントを投稿